§ 1.3. Элементы алгебры логики
Элементы алгебры логики. Вопросы и задания
1. Ознакомьтесь с материалами презентации к параграфу, содержащейся в электронном приложении к учебнику. Дополняет ли презентация информацию, содержащуюся в тексте параграфа?
2. Объясните, почему следующие предложения не являются высказываниями.
1) Какого цвета этот дом?
2) Число X не превосходит единицы.
3) 4Х + 3.
4) Посмотрите в окно.
5) Пейте томатный сок!
6) Эта тема скучна.
7) Рикки Мартин - самый популярный певец.
8) Вы были в театре?
3. Приведите по одному примеру истинных и ложных высказываний из биологии, географии, информатики, истории, математики, литературы.
4. В следующих высказываниях выделите простые высказывания, обозначив каждое из них буквой; запишите с помощью букв и знаков логических операций каждое составное высказывание.
1) Число 376 чётное и трёхзначное.
2) Зимой дети катаются на коньках или на лыжах.
3) Новый год мы встретим на даче или на Красной площади.
4) Неверно, что Солнце движется вокруг Земли.
5) Земля имеет форму шара, который из космоса кажется голубым.
6) На уроке математики старшеклассники отвечали на вопросы учителя, а также писали самостоятельную работу.
5. Постройте отрицания следующих высказываний.
1) Сегодня в театре идёт опера «Евгений Онегин».
2) Каждый охотник желает знать, где сидит фазан.
3) Число 1 есть простое число.
4) Натуральные числа, оканчивающиеся цифрой 0, не являются простыми числами.
5) Неверно, что число 3 не является делителем числа 198.
6) Коля решил все задания контрольной работы.
7) Во всякой школе некоторые ученики интересуются спортом.
8) Некоторые млекопитающие не живут на суше.
6. Пусть А = «Ане нравятся уроки математики» , а В = «Ане нравятся уроки химии» . Выразите следующие формулы на обычном языке:

7. Некоторый сегмент сети Интернет состоит из 1000 сайтов. Поисковый сервер в автоматическом режиме составил таблицу ключевых слов для сайтов этого сегмента. Вот её фрагмент:

По запросу сомики & гуппи было найдено 0 сайтов, по запросу сомики & меченосцы - 20 сайтов, а по запросу меченосцы & гуппи - 10 сайтов.
Сколько сайтов будет найдено по запросу сомики | меченосцы | гуппи ?
Для скольких сайтов рассматриваемого сегмента ложно высказывание «Сомики - ключевое слово сайта ИЛИ меченосцы - ключевое слово сайта ИЛИ гуппи - ключевое слово сайта»?
8. Постройте таблицы истинности для следующих логических выражений:

9. Проведите доказательство рассмотренных в параграфе логических законов с помощью таблиц истинности.
Ключевые слова:
- алгебра логики
- высказывание
- логическая операция
- конъюнкция
- дизъюнкция
- отрицание
- логическое выражение
- таблица истинности
- законы логики
1.3.1. Высказывание
Алгебра в широком смысле этого слова - наука об общих операциях, аналогичных сложению и умножению, которые могут выполняться над разнообразными математическими объектами. Многие математические объекты (целые и рациональные числа, многочлены, векторы, множества) вы изучаете в школьном курсе алгебры, где знакомитесь с такими разделами математики, как алгебра чисел, алгебра многочленов, алгебра множеств и т. д.
Для информатики важен раздел математики, называемый алгеброй логики; объектами алгебры логики являются высказывания.
Например, относительно предложений «Великий русский учёный М. В. Ломоносов родился в 1711 году» и «Two plus six Is eight» можно однозначно сказать, что они истинны. Предложение «Зимой воробьи впадают в спячку» ложно. Следовательно, эти предложения являются высказываниями.
Например, предложение «Это предложение является ложным» не является высказыванием, так как относительно него нельзя сказать, истинно оно или ложно, без того, чтобы не получить противоречие. Действительно, если принять, что предложение истинно, то это противоречит сказанному. Если же принять, что предложение ложно, то отсюда следует, что оно истинно.
Относительно предложения «Компьютерная графика - самая интересная тема в курсе школьной информатики» также нельзя однозначно сказать, истинно оно или ложно. Подумайте сами почему.
Например, не являются высказываниями такие предложения, как: «Запишите домашнее задание», «Как пройти в библиотеку?», «Кто к нам пришёл? ».
Примерами высказываний могут служить:
- «Na - металл» (истинное высказывание);
- «Второй закон Ньютона выражается формулой F=m а» (истинное высказывание);
- «Периметр прямоугольника с длинами сторон a u b равен а b» (ложное высказывание).
Не являются высказываниями числовые выражения, но из двух числовых выражений можно составить высказывание, соединив их знаками равенства или неравенства. Например:
- «34-5 = 2 4» (истинное высказывание);
- «II4-VI > VIII» (ложное высказывание).
Не являются высказываниями и равенства или неравенства, содержащие переменные. Например, предложение «X < 12» становится высказыванием только при замене переменной каким-либо конкретным значением: «5 < 12» - истинное высказывание; «12 < 12» - ложное высказывание.
Обоснование истинности или ложности высказываний решается теми науками, к сфере которых они относятся. Алгебра логики отвлекается от смысловой содержательности высказываний. Её интересует только то, истинно или ложно данное высказывание. В алгебре логики высказывания обозначают буквами и называют логическими переменными. При этом если высказывание истинно, то значение соответствующей ему логической переменной обозначают единицей (А = 1), а если ложно - нулём (Б = 0). 0 и 1, обозначающие значения логических переменных, называются логическими значениями.
Оперируя логическими переменными, которые могут быть равны только 0 или 1, алгебра логики позволяет свести обработку информации к операциям с двоичными данными. Именно аппарат алгебры логики положен в основу компьютерных устройств хранения и обработки информации. С применением элементов алгебры логики вы будете встречаться и во многих других разделах информатики.
1.3.2. Логические операции
Высказывания бывают простые и сложные. Высказывание называется простым, если никакая его часть сама не является высказыванием. Сложные (составные) высказывания строятся из простых с помощью логических операций.
Рассмотрим основные логические операции, определённые над высказываниями. Все они соответствуют связкам, употребляемым в естественном языке.
Конъюнкция
Рассмотрим два высказывания: А = «Основоположником алгебры логики является Джордж Буль», В = «Исследования Клода Шеннона позволили применить алгебру логики в вычислительной технике». Очевидно, новое высказывание «Основоположником алгебры логики является Джордж Буль, и исследования Клода Шеннона позволили применить алгебру логики в вычислительной технике» истинно только в том случае, когда одновременно истинны оба исходных высказывания.
Для записи конъюнкции используются следующие знаки: , , И, &. Например: А В, А В, А И В, А&Б.
Конъюнкцию можно описать в виде таблицы, которую называют таблицей истинности:

В таблице истинности перечисляются все возможные значения исходных высказываний (столбцы А и В), причём соответствующие им двоичные числа, как правило, располагают в порядке возрастания: 00, 01, 10, 11. В последнем столбце записан результат выполнения логической операции для соответствующих операндов.
Иначе конъюнкцию называют логическим умножением. Подумайте почему.
Дизъюнкция
Рассмотрим два высказывания: А = «Идея использования в логике математической символики принадлежит Готфриду Вильгельму Лейбницу», В = «Лейбниц является основоположником бинарной арифметики». Очевидно, новое высказывание «Идея использования в логике математической символики принадлежит Готфриду Вильгельму Лейбницу или Лейбниц является основоположником бинарной арифметики» ложно только в том случае, когда одновременно ложны оба исходных высказывания.
Самостоятельно установите истинность или ложность трёх рассмотренных высказываний.
Для записи дизъюнкции используются следующие знаки: v, |, ИЛИ, +. Например: AvB, А|В, А ИЛИ Б, А+Б.
Дизъюнкция определяется следующей таблицей истинности:

Иначе дизъюнкцию называют логическим сложением. Подумайте почему.
Инверсия
Для записи инверсии используются следующие знаки: НЕ, ¬, ‾. Например: НЕ, ¬, ‾.
Инверсия определяется следующей таблицей истинности:

Инверсию иначе называют логическим отрицанием.
Отрицанием высказывания «У меня дома есть компьютер» будет высказывание «Неверно, что у меня дома есть компьютер» или, что в русском языке то же самое, «У меня дома нет компьютера». Отрицанием высказывания «Я не знаю китайский язык» будет высказывание «Неверно, что я не знаю китайский язык» или, что в русском языке одно и то же, «Я знаю китайский язык». Отрицанием высказывания «Все юноши 9-х классов - отличники» является высказывание «Неверно, что все юноши 9-х классов - отличники», другими словами, «Не все юноши 9-х классов - отличники».
Таким образом, при построении отрицания к простому высказыванию либо используется речевой оборот «неверно, что...», либо отрицание строится к сказуемому, тогда к соответствующему глаголу добавляется частица «не».
Любое сложное высказывание можно записать в виде логического выражения - выражения, содержащего логические переменные, знаки логических операций и скобки. Логические операции в логическом выражении выполняются в следующей очерёдности: инверсия, конъюнкция, дизъюнкция. Изменить порядок выполнения операций можно с помощью расстановки скобок.
Пример 1 . Пусть А = «На Web-странице встречается слово "крейсер"», В = «На Web-странице встречается слово "линкор"». Рассматривается некоторый сегмент сети Интернет, содержащий 5 000 000 Web-страниц. В нём высказывание А истинно для 4800 страниц, высказывание В - для 4500 страниц, а высказывание A v В - для 7000 страниц. Для какого количества Web-страниц в этом случае будут истинны следующие выражения и высказывание?
а) НЕ (А ИЛИ В);
в) На Web-странице встречается слово "крейсер" и не встречается слово " линкор".
Решение . Изобразим множество всех Web-страниц рассматриваемого сектора сети Интернет кругом, внутри которого разместим два круга: одному из них соответствует множество Web-страниц, где истинно высказывание А, второму - где истинно высказывание В (рис. 1.3).

Рис. 1.3.
Графическое изображение множеств Web-страниц
Изобразим графически множества Web-страниц, для которых истинны выражения и высказывание а) - в) (рис. 1.4)

Рис. 1.4.
Графическое изображение множеств Web-страниц, для которых истинны выражения и высказывание а) - в)
Построенные схемы помогут нам ответить на вопросы, содержащиеся в задании.
Выражение А ИЛИ В истинно для 7000 Web-страниц, а всего страниц 5 000 000. Следовательно, выражение А ИЛИ В ложно для 4 993 000 Web-страниц. Иначе говоря, для 4 993 000 Web-страниц истинно выражение НЕ (А ИЛИ В).
Выражение A v B истинно для тех Web-страниц, где истинно А (4800), а также тех Web-страниц, где истинно В (4500). Если бы все Web-страницы были различны, то выражение A v В было бы истинно для 9300 (4800 + 4500) Web-страниц. Но, согласно условию, таких Web-страниц всего 7000. Это значит, что на 2300 (9300 - 7000) Web-страницах встречаются оба слова одновременно. Следовательно, выражение А & В истинно для 2300 Web-страниц.
Чтобы выяснить, для скольких Web-страниц истинно высказывание А и одновременно ложно высказывание В, следует из 4800 вычесть 2300. Таким образом, высказывание «На Web-странице встречается слово "крейсер" И не встречается слово "линкор" » истинно на 2500 Web-страницах.
Самостоятельно запишите логическое выражение, соответствующее рассмотренному высказыванию.
На сайте Федерального центра информационно-образовательных ресурсов (http://fcoir.edu.ru/) размещён информационный модуль «Высказывание. Простые и сложные высказывания. Основные логические операции». Знакомство с этим ресурсом позволит вам расширить представления по изучаемой теме.
1.3.3. Построение таблиц истинности для логических выражений
Для логического выражения можно построить таблицу истинности, показывающую, какие значения принимает выражение при всех наборах значений входящих в него переменных. Для построения таблицы истинности следует:
- подсчитать n - число переменных в выражении;
- подсчитать общее число логических операций в выражении;
- установить последовательность выполнения логических операций с учётом скобок и приоритетов;
- определить число столбцов в таблице: число переменных + число операций;
- заполнить шапку таблицы, включив в неё переменные и операции в соответствии с последовательностью, установленной в п. 3;
- определить число строк в таблице (не считая шапки таблицы) m = 2n;
- выписать наборы входных переменных с учётом того, что они представляют собой целый ряд n-разрядных двоичных чисел от 0 до 2 n - 1;
- провести заполнение таблицы по столбцам, выполняя логические операции в соответствии с установленной последовательностью.
Построим таблицу истинности для логического выражения A v А & В. В нём две переменные, две операции, причём сначала выполняется конъюнкция, а затем - дизъюнкция. Всего в таблице будет четыре столбца:
Наборы входных переменных - это целые числа от О до 3, представленные в двухразрядном двоичном коде: 00, 01, 10, 11. Заполненная таблица истинности имеет вид:

Обратите внимание, что последний столбец (результат) совпал со столбцом А. В таком случае говорят, что логическое выражение A v А & Б равносильно логическому выражению А.
1.3.4. Свойства логических операций
Рассмотрим основные свойства (законы) алгебры логики.
Законы алгебры логики могут быть доказаны с помощью таблиц истинности.
Докажем распределительный закон для логическического сложения:
A v (В & С) = (А V В) & (A v С).
Совпадение столбцов, соответствующих логическим выражениям в левой и правой частях равенства, доказывает справедливость распределительного закона для логического сложения.

Пример 2
. Найдём значение логического выражения ![]() для числа Х = 0.
для числа Х = 0.
Решение . При X = 0 получаем следующее логическое выражение: . Так как логические выражения 0 < 3, 0 < 2 истинны, то, подставив их значения в логическое выражение, получаем: 1&Т = 1&0 = 0.
1.3.5. Решение логических задач
Рассмотрим несколько способов решения логических задач.
Задача 1 . Коля, Вася и Серёжа гостили летом у бабушки. Однажды один из мальчиков нечаянно разбил любимую бабушкину вазу. На вопрос, кто разбил вазу, они дали такие ответы:
Серёжа: 1) Я не разбивал. 2) Вася не разбивал.
Вася: 3) Серёжа не разбивал. 4) Вазу разбил Коля.
Коля: 5) Я не разбивал. 6) Вазу разбил Серёжа.
Бабушка знала, что один из её внуков, назовём его правдивым, оба раза сказал правду; второй, назовём его шутником, оба раза сказал неправду; третий, назовём его хитрецом, один раз сказал правду, а другой раз - неправду. Назовите имена правдивого, шутника и хитреца. Кто из внуков разбил вазу?
Решение. Пусть К = «Коля разбил вазу», В = «Вася разбил вазу», С = «Серёжа разбил вазу». Составим таблицу истинности, с которой представим высказывания каждого мальчика 1 .
-
1 С учётом того, что ваза разбита одним внуком, можно было составлять не всю таблицу, а только её фрагмент, содержащий следуюнще наборы входных переменных: 001, 010, 100.

Исходя из того, что знает о внуках бабушка, следует искать в таблице строки, содержащие в каком-либо порядке три комбинации значений: 00, 11, 01 (или 10). Таких строк в таблице оказалось две (они отмечены галочками). Согласно второй из них, вазу разбили Коля и Вася, что противоречит условию. Согласно первой из найденных строк, вазу разбил Серёжа, он же оказался хитрецом. Шутником оказался Вася. Имя правдивого внука - Коля.
Задача 2 . В соревнованиях по гимнастике участвуют Алла, Валя, Сима и Даша. Болельщики высказали предположения о возможных победителях:
- Сима будет первой, Валя - второй;
- Сима будет второй, Даша - третьей;
- Алла будет второй, Даша - четвёртой.
По окончании соревнований оказалось, что в каждом из предположений только одно из высказываний истинно, другое ложно. Какое место на соревнованиях заняла каждая из девушек, если все они оказались на разных местах?
Решение . Рассмотрим простые высказывания:
C 1 = «Сима заняла первое место»;
В 2 = «Валя заняла второе место»;
С 2 = «Сима заняла второе место»;
Д 3 = «Даша заняла третье место»;
А 2 = «Алла заняла второе место»;
Д 4 = «Даша заняла четвёртое место».
Так как в каждом из трёх предположений одно из высказываний истинно, а другое ложно, то можно заключить следующее:
- C 1 + В 2 = 1, С 1 В 2 = 0;
- С 2 + Д 3 = 1, С 2 Д 3 = 0;
- А 2 + Д 4 = 1, А 2 Д 4 = 0.
Логическое произведение истинных высказываний будет истинным:
(С 1 + В 2) (С 2 + Д 3) (А 2 + Д 4) = 1.
На основании распределительного закона преобразуем левую часть этого выражения:
(С 1 С 2 + С 1 Д 3 + В 2 С 2 + В 2 Д 3) (А 2 + Д 4) = 1.
Высказывание С 1 С 2 означает, что Сима заняла и первое, и второе места. Согласно условию задачи, это высказывание ложно. Ложным является и высказывание В 2 С 2 . Учитывая закон операций с константой 0, запишем:
(С 1 Д 3 + В 2 Д 3) (А 2 +Д 4) = 1.
Дальнейшее преобразование левой части этого равенства и исключение заведомо ложных высказываний дают:
С 1 Д 3 А 2 + С 1 Д 3 Д 4 + В 2 Д 3 А 2 + В 2 Д 3 Д 4 = 1.
C 1 Д 3 А 2 = 1.
Из последнего равенства следует, что С 1 = 1, Д 3 = 1, А 2 = 1. Это означает, что Сима заняла первое место, Алла - второе, Даша - третье. Следовательно, Валя заняла четвёртое место.
Познакомиться с другими способами решения логических задач, а также принять участие в Интернет-олимпиадах и конкурсах по их решению вы сможете на сайте «Математика для школьников» (http://www.kenqyry.com/).
На сайте http://www.kaser.com/ вы сможете скачать демонстрационную версию очень полезной, развивающей логику и умение рассуждать логической головоломки Шерлок.
1.3.6. Логические элементы
Алгебра логики - раздел математики, играющий важную роль в конструировании автоматических устройств, разработке аппаратных и программных средств информационных и коммуникационных технологий.
Вы уже знаете, что любая информация может быть представлена в дискретной форме - в виде фиксированного набора отдельных значений. Устройства, которые обрабатывают такие значения (сигналы), называются дискретными. Дискретный преобразователь, который выдаёт после обработки двоичных сигналов значение одной из логических операций, называется логическим элементом.
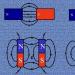
На рис. 1.5 приведены условные обозначения (схемы) логических элементов, реализующих логическое умножение, логическое сложение и инверсию.

Рис 1.5.
Логические элементы
Логический элемент И (конъюнктор) реализует операцию логического умножения (рис. 1.5, а). Единица на выходе этого элемента появится только тогда, когда на всех входах будут единицы.
Логический элемент ИЛИ (дизъюнктор) реализует операцию логического сложения (рис. 1.5, б). Если хотя бы на одном входе будет единица, то на выходе элемента также будет единица.
Логический элемент НЕ (инвертор) реализует операцию отрицания (рис. 1.5, в). Если на входе элемента О, то на выходе 1 и наоборот.
Компьютерные устройства, производящие операции над двоичными числами, и ячейки, хранящие данные, представляют собой электронные схемы, состоящие из отдельных логических элементов. Более подробно эти вопросы будут раскрыты в курсе информатики 10-11 классов.
Пример 3 . Проанализируем электронную схему, т. е. выясним, какой сигнал должен быть на выходе при каждом возможном наборе сигналов на входах.

Решение . Все возможные комбинации сигналов на входах А к В внесём в таблицу истинности. Проследим преобразование каждой пары сигналов при прохождении их через логические элементы и запишем полученный результат в таблицу. Заполненная таблица истинности полностью описывает рассматриваемую электронную схему.

Таблицу истинности можно построить и по логическому выражению, соответствующему электронной схеме. Последний логический элемент в рассматриваемой схеме - конъюнктор. В него поступают сигналы от входа Л и от инвертора. В свою очередь, в инвертор поступает сигнал от входа В. Таким образом,
Составить более полное представление о логических элементах и электронных схемах вам поможет работа с тренажёром «Логика» (http://kpolyakov. narod. ru/prog/logic. htm).
Самое главное
Высказывание - это предложение на любом языке, содержание которого можно однозначно определить как истинное или ложное.
Основные логические операции, определённые над высказываниями: инверсия, конъюнкция, дизъюнкция.

Таблицы истинности для основных логических операций:

При вычислении логических выражений сначала выполняются действия в скобках. Приоритет выполнения логических операций:
Вопросы и задания

1. Заполните таблицу, записав в десятичной позиционной системе счисления числа, соответствующие числам, записанным в римской системе счисления:
2. Переведите числа из римской системы счисления в десятичную систему счисления:

3. Запишите в римской системе счисления:

4. Запишите алфавиты следующих позиционных систем счисления:

5. Алфавиты каких позиционных систем счисления приведены ниже? Запишите их названия:

6. Запишите наименьшее основание системы счисления, в которой могут быть записаны следующие числа:

7. Запишите числа в развёрнутом виде:

8. Вычислите десятичные эквиваленты следующих чисел:

9. Вычислите десятичные эквиваленты следующих двоичных чисел:

10. Запишите максимальное и минимальное четырёхзначные числа:

11. Калькулятор, работающий в троичной системе счисления, имеет пять знакомест для вывода числа на экран. С каким самым большим десятичным числом можно работать на этом калькуляторе?

12. Укажите номера чисел по возрастанию:

13. Сравните числа:

14. Вычислите х, для которых верны равенства:

15. Один мудрец писал: «Мне 33 года. Моей матери 124 года, а отцу 131 год. Вместе нам 343 года». Какую систему счисления использовал мудрец и сколько ему лет?

16. Один человек имел 102 монеты. Он поровну разделил их между двумя своими детьми. Каждому досталось по 12 монет и одна осталась лишней. Какая система счисления использовалась и сколько было монет?

17. Постройте на координатной плоскости рисунок, отметив и соединив точки в указанной последовательности.

18. Постройте на координатной плоскости рисунок, отметив и последовательно соединив точки:

19. Постройте на координатной плоскости рисунок, отметив и последовательно соединив точки:

20. Переведите целые числа из десятичной системы счисления в двоичную:

21. Переведите целые числа из десятичной системы счисления в двоичную, используя метод разностей:

22. Дешифруйте графическое изображение, представив следующие десятичные числа в двоичном коде (каждую двоичную цифру вписывайте в отдельную клетку; клетки с нулями заштрихуйте):

23. Сколько 1 в двоичной записи десятичного числа?

24. Сколько 0 в двоичной записи десятичного числа?

25. Выпишите натуральные целые числа, принадлежащие следующим числовым промежуткам:

26. Переведите целые числа из десятичной системы счисления в восьмеричную:

27. Переведите целые числа из десятичной системы счисления в шестнадцатеричную:

28. Заполните таблицу, в каждой строке которой одно и то же число должно быть записано в системах счисления с основанием 2, 8, 10 и 16.

29. Выполните операцию сложения над двоичными числами. Выполните проверку, переведя слагаемые и сумму в десятичную систему счисления.

30. Выполните операцию умножения над двоичными числами. Выполните проверку, переведя сомножители и произведение в десятичную систему счисления.

31. Разработайте таблицы сложения и умножения для восьмеричной системы счисления.

32. Решите уравнение

33. В олимпиаде по информатике участвовало 30 девочек и 50 мальчиков, а всего – 100 человек. В какой системе счисления записаны эти сведения?

34. Найдите значение выражения K+L+M+N в восьмеричной системе счисления, если:

35. Постройте граф, отражающий взаимосвязи основных понятий по теме «Системы счисления».

36. Переведите число 1010 из десятичной системы счисления в двоичную систему счисления. Сколько единиц содержит полученное число? В ответе укажите одно число – количество единиц.
Ответ: 7.
37. Представьте десятичные числа в беззнаковом 8-разрядном формате.

38. Запишите прямой код десятичных чисел в 8-разрядном формате со знаком.

39. Найдите десятичные эквиваленты чисел по их прямым кодам, записанным в 8-разрядном формате со знаком:

40. Запишите следующие числа в естественной форме:

41. Запишите число 2014,4102(10) пятью различными способами в нормальной форме:

42. Запишите следующие числа в нормальной форме с нормализованной мантиссой – правильной дробью, имеющей после запятой цифру, отличную от нуля:

43. Рассмотрите фрагмент кодировочной таблицы ASCII:

Декодируйте с помощью кодировочной таблицы следующие тексты:

{reklama}
44. Перейдите от десятичного кода к шестнадцатеричному и декодируйте следующие тексты:

45. Реферат, набранный на компьютере, содержит 16 страниц, на каждой странице 32 строки, в каждой строке 64 символа. Определите информационный объём статьи в кодировке Unicode, где каждый символ кодируется 16 битами.

46. Каждой шестнадцатеричной цифре поставлена в соответствие цепочка из четырёх 0 и 1 (двоичная тетрада):
Декодируйте графические изображения, заменяя каждую шестнадцатеричную цифру двоичной тетрадой. Закрасьте клеточки с нулями.

47. Вычислите необходимый объём видеопамяти для графического режима, если разрешение экрана монитора 1024х768, глубина цвета 32 бита.

48. Вычислите необходимый объём видеопамяти для графического режима, если разрешение экрана монитора 1024х768, а количество цветов в палитре 256.

49. Для хранения растрового изображения размером 128х64 пикселя отвели 8 Кбайт памяти. Какое максимально возможное количество цветов в палитре изображения?

50. Статья, набранная на компьютере, содержит 4 страницы, на каждой странице 40 строк, в каждой строке 64 символа. В одном из представлений Unicode каждый символ кодируется 16 битами. Определите информационный объём статьи в этом варианте представления Unicode.
Ответ: 1) 20 Кбайт.
51. Запишите по одному истинному и одному ложному высказыванию из биологии, географии, информатики, истории, математики, литературы:

52. В следующих высказываниях выделите простые, обозначив каждое из них буквой; запишите с помощью букв и знаков логических операций каждое составное высказывание.

53. В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.

Какое количество страниц (в тысячах) будет найдено по запросу ШОКОЛАД?

54. В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.

Какое количество страниц (в тысячах) будет найдено по запросу ЗУБР | ТУР?
Решите задачу, используя круги Эйлера:

55. В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.

Какое количество страниц (в тысячах) будет найдено по запросу ФУТБОЛ&ХОККЕЙ?
Решите задачу, используя круги Эйлера:

56. Некоторый сегмент сети Интернет состоит из 1000 сайтов. В таблице приведены запросы и количество найденных по ним страниц в этом сегменте сети:

Сколько байтов будет найдено по запросу ЧЕРНИКА | МАЛИНА|БРУСНИКА?
Решите задачу, используя круги Эйлера:

60. Найдите значение логического выражения для указанных значений Х:

61. Заполните таблицу логическими значениями:

62. Три друга играли во дворе в футбол и разбили мячом окно. Ваня сказал: «Это я разбил окно, Коля окно не разбивал». Коля сказал: «Это сделал не я и не Саша». Саша сказал: «Это сделал не я и не Ваня». А бабушка сидела на лавочке и всё видела. Она сказала, что только один мальчик оба раза сказал правду, но не назвала того, кто разбил окно. Кто же это?

63. Расследуется дело о хищении. В этом преступлении подозреваются Брагин, Кургин и Лиходеев. Каждый из них дал следующие показания.
Брагин: «Я не делал этого. Это сделал Лиходеев».
Лиходеев: «Я не виноват, но и Кургин тут ни при чём».
Кургин: «Лиходеев не виновен. Преступление совершил Брагин».
Следствием точно установлено, что хищение совершили двое, кроме того, подозреваемые путались в показаниях и каждый из них не дал полностью правдивых показаний. Кто же совершил преступление?
Решите задачу, заполнив и проанализировав таблицу истинности:

64. В поездке пятеро друзей – Антон, Борис, Вадим, Дима и Гриша – знакомились с попутчицей. Они предложили ей отгадать их фамилии, причём каждый из них высказал одно истинное и одно ложное утверждение:
Дима сказал: «Моя фамилия – Мишин, а фамилия Бориса - Хохлов».
Антон сказал: «Мишин – это моя фамилия, а фамилия Вадима - Белкин». Борис сказал: «Фамилия Вадима – Тихонов, а моя фамилия - Мишин».
Вадим сказал: «Моя фамилия – Белкин, а фамилия Гриши - Чехов».
Гриша сказал: «Да, моя фамилия Чехов, а фамилия Антона - Тихонов».
Какую фамилию носит каждый из друзей?
(Дм(¬Бх)+(¬Дм)Бх)*(Ам(¬Вб)+(¬Ам)Вб)*(Бм(¬Вт)+(¬Бм)Вт)*(Вб(¬Гч)+(¬Вб)Гч)*(Гч(¬Ат)+(¬Гч)Ат)=1
Выражение истинно тогда, когда все суммы истинны. Допустим, что Дм=1, тогда Ам=0, Бм=0; Но тогда Вб=1 и Вт=1, что невозможно. Значит, Бх-истина. Тогда Бм-ложно, Вт-истинно, Ат-ложно, Гч – истинно, Вб – ложно, Ам – истинно.
Ответ: Борис Хохлов, Вадим Тихонов, Гриша Чехов, Антон Мишин, Дима Белкин.
65. Трое друзей, футбольных болельщиков, спорили о результатах предстоящего турнира.
Мнение Юрия: «Вот увидите, «Барселона» не станет первой. «Зенит» будет первым».
Мнение Виктора: «Победителем будет «Барселона». А о «Зените» и говорить нечего, ему не быть первым».
Мнение Леонида: «Первого места «Реалу» не видать, а вот у «Барселоны» есть все шансы на победу».
По завершении соревнований оказалось, что каждое из двух предположений двоих друзей подтвердилось, а оба предположения третьего из друзей оказались неверны. Кто выиграл турнир?
Решите задачу, составив и преобразовав логическое выражение:

66. Выясните, какой сигнал должен быть на выходе схемы при каждом возможном наборе сигналов на входах. Заполните таблицу работы схемы. Каким логическим выражением описывается схема?

67. Для какого из приведённых имён истинно высказывание:
Формулы и законы логики
На вводном уроке, посвящённом основам математической логики , мы познакомились с базовыми понятиями этого раздела математики, и сейчас тема получает закономерное продолжение. Помимо нового теоретического, а точнее даже не теоретического – а общеобразовательного материала нас ожидают практические задания, и поэтому если вы зашли на данную страницу с поисковика и/или плохо ориентируетесь в материале, то, пожалуйста, пройдите по вышеуказанной ссылке и начните с предыдущей статьи. Кроме того, для практики нам потребуется 5 таблиц истинности логических операций , которые я настоятельно рекомендую переписать от руки .
НЕ запомнить, НЕ распечатать, а именно ещё раз осмыслить и собственноручно переписать на бумагу – чтобы они были перед глазами:
– таблица НЕ;
– таблица И;
– таблица ИЛИ;
– импликационная таблица;
– таблица эквиваленции.
Это очень важно. В принципе, их было бы удобно занумеровать «Таблица 1», «Таблица 2» и т.д. , но я неоднократно подчёркивал изъян такого подхода – как говорится, в одном источнике таблица окажется первой, а в другом – сто первой. Поэтому будем использовать «натуральные» названия. Продолжаем:
На самом деле с понятием логической формулы вы уже знакомы. Приведу стандартное, но довольно-таки остроумное определение : формулами алгебры высказываний называются:
1) любые элементарные (простые) высказывания ;
2) если и – формулы, то формулами также являются выражения вида
.
Никаких других формул нет.
В частности формулой является любая логическая операция, например логическое умножение . Обратите внимание на второй пункт – он позволяет рекурсивным
образом «создать» сколь угодно длинную формулу. Поскольку ![]() – формулы, то – тоже формула; так как и – формулы, то
– формулы, то – тоже формула; так как и – формулы, то ![]() – тоже формула и т.д. Любое элементарное высказывание (опять же согласно определению)
может входить в формулу неоднократно.
– тоже формула и т.д. Любое элементарное высказывание (опять же согласно определению)
может входить в формулу неоднократно.
Формулой не является, например, запись – и здесь прослеживается очевидная аналогия с «алгебраическим мусором» , из которого не понятно – нужно ли числа складывать или умножать.
Логическую формулу можно рассматривать, как логическую функцию
. Запишем в функциональном виде ту же конъюнкцию:![]()
Элементарные высказывания и в этом случае играют роль аргументов (независимых переменных), которые в классической логике могут принимать 2 значения: истина или ложь . Далее для удобства я буду иногда называть простые высказывания переменными .
Таблица, описывающая логическую формулу (функцию) называется, как уже было озвучено, таблицей истинности
. Пожалуйста – знакомая картинка:
Принцип формирования таблицы истинности таков: «на входе» нужно перечислить все возможные комбинации
истины и лжи, которые могут принимать элементарные высказывания (аргументы). В данном случае в формулу входят два высказывания, и нетрудно выяснить, что таких комбинаций четыре. «На выходе» же получаем соответствующие логические значения всей формулы (функции).
Надо сказать, что «выход» здесь получился «в один шаг», но в общем случае логическая формула является более сложной. И в таких «непростых случаях» нужно соблюдать порядок выполнения логических операций :
– в первую очередь выполняется отрицание ;
– во вторую очередь – конъюнкция ;
– затем – дизъюнкция ;
– потом импликация ;
– и, наконец, низший приоритет имеет эквиваленция .
Так, например, запись подразумевает, что сначала нужно осуществить логическое умножение , а затем – логическое сложение: . Прямо как в «обычной» алгебре – «сначала умножаем, а затем складываем».
Порядок действий можно изменить привычным способом – скобками:
– здесь в первую очередь выполняется дизъюнкция и только потом более «сильная» операция.
Наверное, все понимают, но на всякий пожарный : и – это две разные формулы! (как в формальном, так и в содержательном плане)
Составим таблицу истинности для формулы . В данную формулу входят два элементарных высказывания и «на входе» нам нужно перечислить все возможные комбинации единиц и нулей. Чтобы избежать путаницы и разночтений договоримся перечислять комбинации строго в таком порядке
(который я, собственно, де-факто использую с самого начала)
:
В формулу входят две логические операции, и согласно их приоритету, в первую очередь нужно выполнить отрицание
высказывания . Ну что же, отрицаем столбец «пэ» – единицы превращаем в нули, а нули – в единицы:
На втором шаге смотрим на столбцы и и применяем к ним операцию ИЛИ
. Немного забегая вперёд, скажу, что дизъюнкция перестановочна ( и – это одно и то же)
, и поэтому столбцы можно анализировать в привычном порядке – слева направо. При выполнении логического сложения удобно использовать следующее прикладное рассуждение: «Если два нуля – ставим ноль, если хотя бы одна единица – единицу»
:
Таблица истинности построена. А теперь вспомним старую-добрую импликацию:
…внимательно-внимательно… смотрим на итоговые колонки…. В алгебре высказываний такие формулы называются равносильными
или тождественными
:
(три горизонтальные чёрточки – это значок тождества)
В 1-й части урока я обещал выразить импликацию через базовые логические операции, и выполнение обещания не заставило себя ждать! Желающие могут вложить в импликацию содержательный смысл (например, «Если идёт дождь, то на улице сыро») и самостоятельно проанализировать равносильное утверждение .
Сформулируем общее определение : две формулы называются равносильными (тождественными) , если они принимают одинаковые значения при любом наборе значений, входящих в эти формулы переменных (элементарных высказываний) . Также говорят, что «формулы равносильны, если совпадают их таблицы истинности» , но мне не очень нравится эта фраза.
Задание 1
Составить таблицу истинности для формулы и убедиться в справедливости знакомого вам тождества .
Ещё раз повторим порядок решения задачи:
1) Так как в формулу входят две переменные, то всего будет 4 возможных набора нулей и единиц. Записываем их в оговорённом выше порядке.
2) Импликации «слабее» конъюнкции, но они располагаются в скобках. Заполняем столбец , при этом удобно использовать следующее прикладное рассуждение: «если из единицы следует ноль, то ставим ноль, во всех других случаях – единицу» . Далее заполняем столбец для импликации , и при этом, внимание! – столбцы и следует анализировать «справа налево»!
3) И на завершающем этапе заполняем итоговый столбец . А здесь удобно рассуждать так: «если в столбцах и две единицы, то ставим единицу, во всех остальных случаях – ноль» .
И, наконец, сверяемся с таблицей истинности эквиваленции .
Основные равносильности алгебры высказываний
С двумя из них мы только что познакомились, но ими дело, понятно, не огранивается. Тождеств довольно много и я перечислю самые важные и самые известные из них:
Коммутативность конъюнкции и коммутативность дизъюнкции
Коммутативность
– это перестановочность:
Знакомые с 1-го класса правила: «От перестановки множителей (слагаемых) произведение (сумма) не меняется» . Но при всей кажущейся элементарности этого свойства, справедливо оно далеко не всегда, в частности, некоммутативным является умножение матриц (в общем случае их переставлять нельзя) , а векторное произведение векторов – антикоммутативно (перестановка векторов влечёт за собой смену знака) .
И, кроме того, здесь я снова хочу подчеркнуть формализм математической логики. Так, например, фразы «Студент сдал экзамен и выпил» и «Студент выпил и сдал экзамен» различны с содержательной точки зрения, но неразличимы с позиций формальной истинности. …Таких студентов знает каждый из нас, и из этических соображений мы не будет озвучивать конкретных имён =)
Ассоциативность логического умножения и сложения
Или, если «по-школьному» – сочетательное свойство:
Дистрибутивные свойства
Обратите внимание, что во 2-м случае будет некорректно говорить о «раскрытии скобок», в известном смысле здесь «фикция» – ведь их можно убрать вообще: , т.к. умножение – это более сильная операция.
И опять же – эти, казалось бы, «банальные» свойства выполняются далеко не во всех алгебраических системах, и, более того, требуют доказательства (о которых мы очень скоро поговорим) . К слову, второй дистрибутивный закон несправедлив даже в нашей «обычной» алгебре. И в самом деле:
Закон идемпотентности
Что делать, латынь....
Прямо какой-то принцип здоровой психики: «я и я – это я», «я или я – это тоже я» =)
И тут же несколько похожих тождеств:![]()
…мда, что-то я даже подзавис… так и доктором философии завтра можно проснуться =)
Закон двойного отрицания
Ну а здесь уже напрашивается пример с русским языком – все прекрасно знают, что две частицы «не» означают «да». А для того, чтобы усилить эмоциональную окраску отрицания нередко используют три «не»:
– даже с крохотным доказательством получилось!
Законы поглощения
– «а был ли мальчик?» =)
В правом тождестве скобки можно опустить.
Законы де Моргана
Предположим, что строгий Преподаватель (имя которого вам тоже известно:)) ставит экзамен, если – Студент ответил на 1-й вопрос и – Студент ответил на 2-й вопрос . Тогда высказывание , гласящее о том, что Студент не сдал экзамен , будет равносильно утверждению – Студент не ответил на 1-й вопрос или на 2-й вопрос .
Как уже отмечалось выше, равносильности подлежат доказательству, которое стандартно осуществляется с помощью таблиц истинности. В действительности мы уже доказали равносильности, выражающие импликацию и эквиваленцию, и сейчас настало время закрепить технику решения данной задачи.
Докажем тождество . Поскольку в него входит единственное высказывание , то «на входе» возможно всего лишь два варианта: единица либо ноль. Далее приписываем единичный столбец и применяем к ним правило И
:
В результате «на выходе» получена формула, истинность которой совпадает с истинностью высказывания . Равносильность доказана.
Да, это доказательство является примитивным (а кто-то скажет, что и «тупым») , но типичный Преподаватель по матлогике вытрясет за него душу. Поэтому даже к таким простым вещам не стОит относиться пренебрежительно.
Теперь убедимся, например, в справедливости закона де Моргана .
Сначала составим таблицу истинности для левой части. Поскольку дизъюнкция находится в скобках, то в первую очередь выполняем именно её, после чего отрицаем столбец :
Далее составим таблицу истинности для правой части . Здесь тоже всё прозрачно – в первую очередь проводим более «сильные» отрицания, затем применяем к столбцам правило И
:
Результаты совпали, таким образом, тождество доказано.
Любую равносильность можно представить в виде тождественно истинной формулы
. Это значит, что ПРИ ЛЮБОМ исходном наборе нулей и единиц
«на выходе» получается строго единица. И этому есть очень простое объяснение: так как таблицы истинности и совпадают, то, разумеется, они эквивалентны.Соединим, например, эквиваленцией левую и правую часть только что доказанного тождества де Моргана:
Или, если компактнее:
Задание 2
Доказать следующие равносильности:
б) ![]()
Краткое решение в конце урока. Не ленимся! Постарайтесь не просто составить таблицы истинности, но ещё и чётко сформулировать выводы. Как я недавно отмечал, пренебрежение простыми вещами может обойтись очень и очень дорого!
Продолжаем знакомиться с законами логики!
Да, совершенно верно – мы с ними уже вовсю работаем:
Истина при , называется тождественно истинной формулой или законом логики .
В силу обоснованного ранее перехода от равносильности к тождественно истинной формуле , все перечисленные выше тождества представляют собой законы логики.
Формула, которая принимает значение Ложь при любом наборе значений входящих в неё переменных , называется тождественно ложной формулой или противоречием .
Фирменный пример противоречия от древних греков:
– никакое высказывание не может быть истинным и ложным одновременно.
Доказательство тривиально:
«На выходе» получены исключительно нули, следовательно, формула действительно тождественна ложна
.
Однако и любое противоречие – это тоже закон логики, в частности: ![]()
Нельзя объять столь обширную тему в одной-единственной статье, и поэтому я ограничусь ещё лишь несколькими законами:
Закон исключённого третьего
– в классической логике любое высказывание истинно или ложно и третьего не дано. «Быть или не быть» – вот в чём вопрос.
Самостоятельно составьте табличку истинности и убедитесь в том, что это тождественно истинная формула.
Закон контрапозиции
Этот закон активно муссировался, когда мы обсуждали суть необходимого условия , вспоминаем: «Если во время дождя на улице сыро, то из этого следует, что если на улице сухо, то дождя точно не было» .
Также из данного закона следует, что если справедливой является прямая теорема , то обязательно истинным будет и утверждение , которое иногда называют противоположной теоремой.
Если истинна обратная теорема , то в силу закона контрапозиции , справедлива и теорема, противоположная обратной :
И снова вернёмся к нашим содержательным примерам: для высказываний – число делится на 4, – число делится на 2 справедливы прямая и противоположная теоремы, но ложны обратная и противоположная обратной теоремы. Для «взрослой» же формулировки теоремы Пифагора истинны все 4 «направления».
Закон силлогизма
Тоже классика жанра: «Все дубы – деревья, все деревья – растения, следовательно, все дубы – растения» .
Ну и здесь опять хочется отметить формализм математической логики: если наш строгий Преподаватель думает, что некий Студент – есть дуб, то с формальной точки зрения данный Студент, безусловно, растение =) …хотя, если задуматься, то может быть и с неформальной тоже =)
Составим таблицу истинности для формулы . В соответствии с приоритетом логических операций, придерживаемся следующего алгоритма:
1) выполняем импликации и . Вообще говоря, можно сразу выполнить и 3-ю импликацию, но с ней удобнее (и допустимо!) разобраться чуть позже;
2) к столбцам применяем правило И ;
3) вот теперь выполняем ;
4) и на завершающем шаге применяем импликацию к столбцам ![]() и .
и .
Не стесняйтесь контролировать процесс указательным и средним пальцем:))
Из последнего столбца, думаю, всё понятно без комментариев:
, что и требовалось доказать.
Задание 3
Выяснить, будет ли являться законом логики следующая формула:
Краткое решение в конце урока. Да, и чуть не забыл – давайте условимся перечислять исходные наборы нулей и единиц в точно таком же порядке, что и при доказательстве закона силлогизма. Строки конечно, можно и переставить, но это сильно затруднит сверку с моим решением.
Преобразование логических формул
Помимо своего «логического» назначения, равносильности широко используются для преобразования и упрощения формул. Грубо говоря, одну часть тождества можно менять на другую. Так, например, если в логической формуле вам встретился фрагмент , то по закону идемпотентности вместо него можно (и нужно) записать просто . Если вы видите , то по закону поглощения упрощайте запись до . И так далее.
Кроме того, есть ещё одна важная вещь: тождества справедливы не только для элементарных высказываний, но и для произвольных формул. Так, например:
![]()
![]()
, где – любые (сколь угодно сложные)
формулы.
Преобразуем, например, сложную импликацию ![]() (1-е тождество)
:
(1-е тождество)
:
Далее применим к скобке «сложный» закон де Моргана, при этом, в силу приоритета операций, именно закон , где ![]() :
:
Скобки можно убрать, т.к. внутри находится более «сильная» конъюнкция:
Ну, а с коммутативностью вообще всё просто – даже обозначать ничего не нужно… что-то запал мне в душу закон силлогизма:))
Таким образом, закон можно переписать и в более затейливом виде:
Проговорите вслух логическую цепочку «с дубом, деревом, растением», и вы поймёте, что от перестановки импликаций содержательный смысл закона нисколько не изменился. Разве что формулировка стала оригинальнее.
В качестве тренировки упросим формулу .
С чего начать? Прежде всего, разобраться с порядком действий: здесь отрицание применено к целой скобке, которая «скреплена» с высказыванием «чуть более слабой» конъюнкцией. По существу, перед нами логическое произведение двух множителей: . Из двух оставшихся операций низшим приоритетом обладает импликация, и поэтому вся формула имеет следующую структуру: .
Как правило, на первом шаге (шагах) избавляются от эквиваленции и импликации (если они есть) и сводят формулу к трём основным логическим операциям. Что тут скажешь…. Логично.
(1) Используем тождество ![]() . А нашем случае .
. А нашем случае .
Затем обычно следуют «разборки» со скобками. Сначала всё решение, затем комментарии. Чтобы не получилось «масло масляное», буду использовать значки «обычного» равенства:
(2) К внешним скобкам применяем закон де Моргана , где .